106 : Nonlinear Diffusion
This example solves the nonlinear diffusion equation
\[\begin{aligned} u_t - \Delta u^m & = 0 \end{aligned}\]
in $\Omega := (-1,1)$ with homogeneous Neumann boundary conditions.
The solution looks like this:
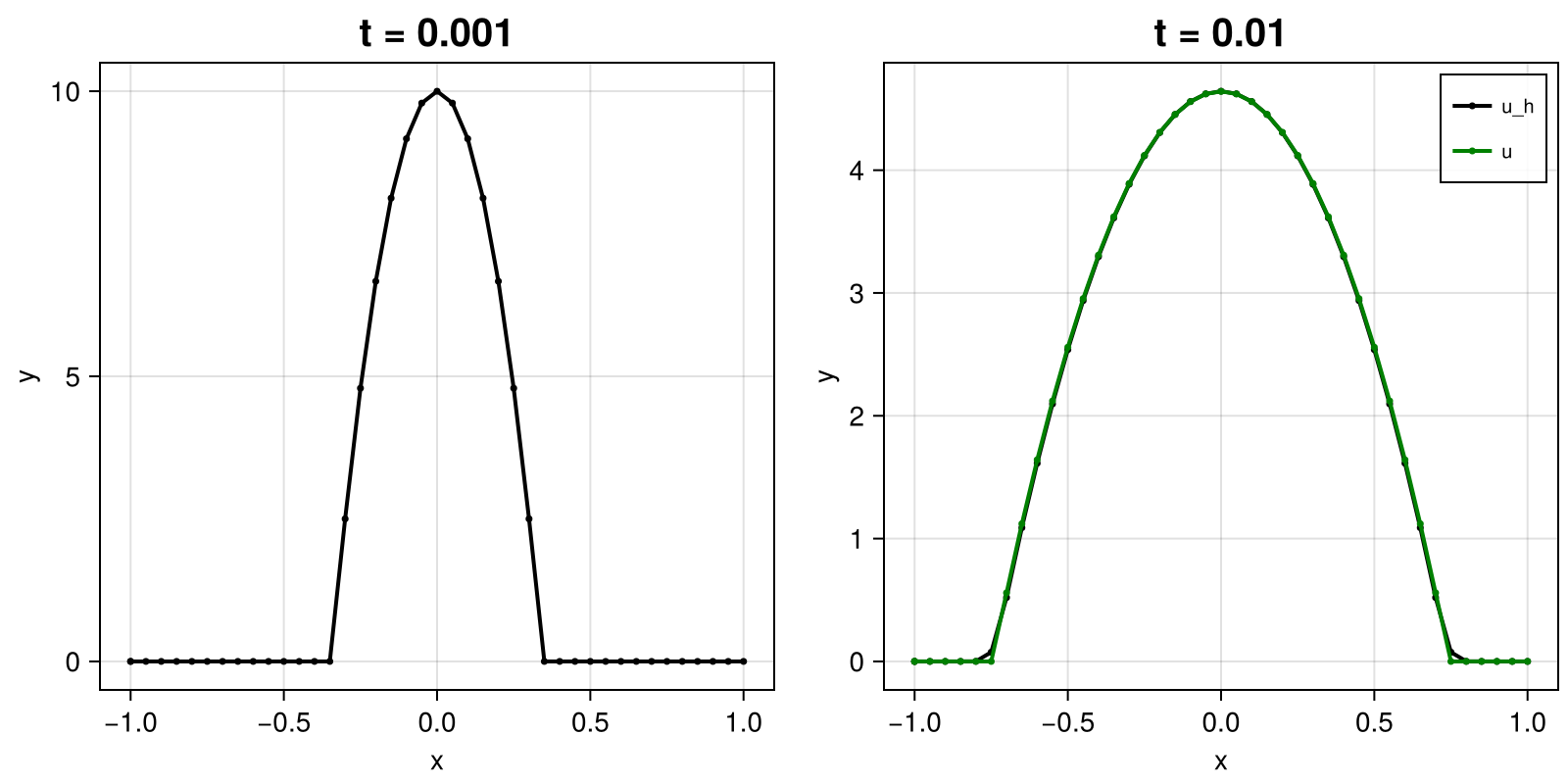
module Example106_NonlinearDiffusion
using ExtendableFEM
using ExtendableGrids
using DifferentialEquations
using GridVisualize
# Barenblatt solution
# (see Barenblatt, G. I. "On nonsteady motions of gas and fluid in porous medium." Appl. Math. and Mech.(PMM) 16.1 (1952): 67-78.)
function u_exact!(result, qpinfo)
t = qpinfo.time
x = qpinfo.x[1]
m = qpinfo.params[1]
tx = t^(-1.0 / (m + 1.0))
xx = x * tx
xx = xx * xx
xx = 1 - xx * (m - 1) / (2.0 * m * (m + 1))
if xx < 0.0
xx = 0.0
end
result[1] = tx * xx^(1.0 / (m - 1.0))
end
function kernel_nonlinear!(result, input, qpinfo)
u, ∇u = input[1], input[2]
m = qpinfo.params[1]
result[1] = m * u^(m - 1) * ∇u
end
# everything is wrapped in a main function
function main(;
m = 2,
h = 0.05,
t0 = 0.001,
T = 0.01,
order = 1,
τ = 0.0001,
Plotter = nothing,
use_diffeq = true,
use_masslumping = true,
solver = ImplicitEuler(autodiff = false),
kwargs...)
# load mesh and exact solution
xgrid = simplexgrid(-1:h:1)
# set finite element types [surface height, velocity]
FEType = H1Pk{1, 1, order}
# generate empty PDEDescription for three unknowns (h, u)
PD = ProblemDescription("Nonlinear Diffusion Equation")
u = Unknown("u"; name = "u")
assign_unknown!(PD, u)
assign_operator!(PD, NonlinearOperator(kernel_nonlinear!, [grad(u)], [id(u), grad(u)]; params = [m], bonus_quadorder = 2))
# prepare solution vector and initial data
FES = FESpace{FEType}(xgrid)
sol = FEVector(FES; tags = PD.unknowns)
interpolate!(sol[u], u_exact!; time = t0, params = [m])
# init plotter and plot u0
plt = GridVisualizer(; Plotter = Plotter, layout = (1, 2), size = (800,400))
scalarplot!(plt[1, 1], id(u), sol; label = "u_h", markershape = :circle, markevery = 1, title = "t = $t0")
# generate mass matrix (with mass lumping)
M = FEMatrix(FES)
assemble!(M, BilinearOperator([id(1)]; lump = 2 * use_masslumping))
if (use_diffeq)
# generate ODE problem
prob = ExtendableFEM.generate_ODEProblem(PD, FES, (t0, T); init = sol, mass_matrix = M.entries.cscmatrix)
# solve ODE problem
de_sol = DifferentialEquations.solve(prob, solver, abstol = 1e-6, reltol = 1e-3, dt = τ, dtmin = 1e-8, adaptive = true)
@info "#tsteps = $(length(de_sol))"
# get final solution
sol.entries .= de_sol[end]
else
# add backward Euler time derivative
assign_operator!(PD, BilinearOperator(M, [u]; factor = 1 / τ, kwargs...))
assign_operator!(PD, LinearOperator(M, [u], [u]; factor = 1 / τ, kwargs...))
# generate solver configuration
SC = SolverConfiguration(PD, FES; init = sol, maxiterations = 1, kwargs...)
# iterate tspan
t = 0
for it ∈ 1:Int(floor((T - t0) / τ))
t += τ
ExtendableFEM.solve(PD, FES, SC; time = t)
end
end
# plot final state and exact solution for comparison
scalarplot!(plt[1, 2], id(u), sol; label = "u_h", markershape = :circle, markevery = 1)
interpolate!(sol[1], u_exact!; time = T, params = [m])
scalarplot!(plt[1, 2], id(u), sol; clear = false, color = :green, label = "u", title = "t = $T", legend = :best)
return sol, plt
end
endThis page was generated using Literate.jl.