205 : Heat equation
This example computes the solution $u$ of the two-dimensional heat equation
\[\begin{aligned} u_t - \Delta u & = 0 \quad \text{in } \Omega \end{aligned}\]
for homogeneous Dirichlet boundary conditions and some given initial state on the unit square domain $\Omega$ on a given grid.
The initial condition and the final solution for the default parameters looks like this:
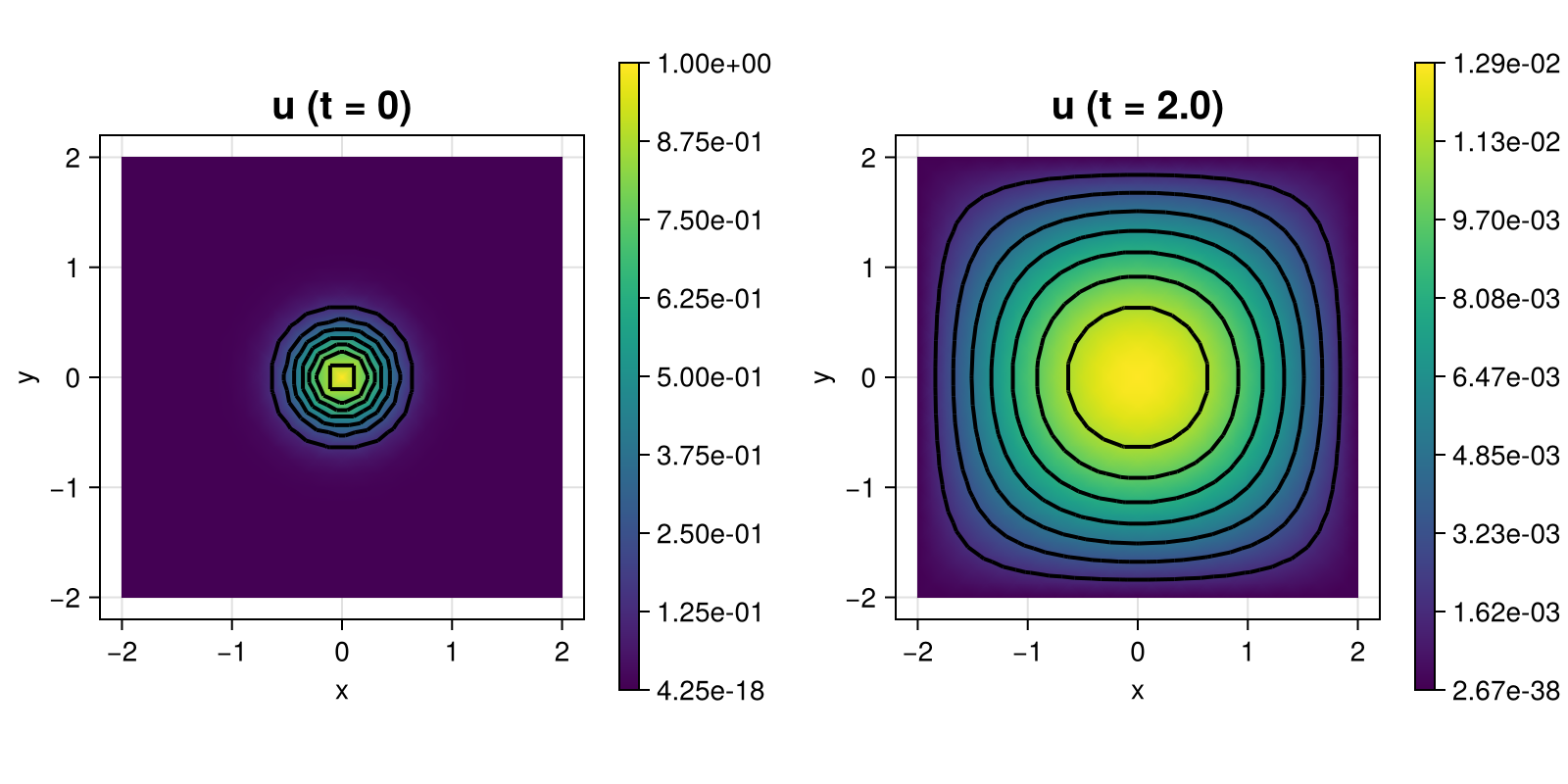
module Example205_HeatEquation
using ExtendableFEM
using ExtendableGrids
using DifferentialEquations
# initial state u at time t0
function initial_data!(result, qpinfo)
x = qpinfo.x
result[1] = exp(-5 * x[1]^2 - 5 * x[2]^2)
end
function main(; nrefs = 4, T = 2.0, τ = 1e-3, order = 2, use_diffeq = true,
solver = ImplicitEuler(autodiff = false), Plotter = nothing, kwargs...)
# problem description
PD = ProblemDescription("Heat Equation")
u = Unknown("u")
assign_unknown!(PD, u)
assign_operator!(PD, BilinearOperator([grad(u)]; store = true, kwargs...))
assign_operator!(PD, HomogeneousBoundaryData(u; regions = 1:4))
# grid
xgrid = uniform_refine(grid_unitsquare(Triangle2D; scale = [4, 4], shift = [-0.5, -0.5]), nrefs)
# prepare solution vector and initial data u0
FES = FESpace{H1Pk{1, 2, order}}(xgrid)
sol = FEVector(FES; tags = PD.unknowns)
interpolate!(sol[u], initial_data!; bonus_quadorder = 5)
# init plotter and plot u0
plt = plot([id(u)], sol; add = 1, Plotter = Plotter, title_add = " (t = 0)")
if (use_diffeq)
# generate DifferentialEquations.ODEProblem
prob = generate_ODEProblem(PD, FES, (0.0, T); init = sol, constant_matrix = true)
# solve ODE problem
de_sol = DifferentialEquations.solve(prob, solver, abstol = 1e-6, reltol = 1e-3, dt = τ, dtmin = 1e-6, adaptive = true)
@info "#tsteps = $(length(de_sol))"
# get final solution
sol.entries .= de_sol[end]
else
# add backward Euler time derivative
M = FEMatrix(FES)
assemble!(M, BilinearOperator([id(1)]))
assign_operator!(PD, BilinearOperator(M, [u]; factor = 1 / τ, kwargs...))
assign_operator!(PD, LinearOperator(M, [u], [u]; factor = 1 / τ, kwargs...))
# generate solver configuration
SC = SolverConfiguration(PD, FES; init = sol, maxiterations = 1, constant_matrix = true, kwargs...)
# iterate tspan
t = 0
for it ∈ 1:Int(floor(T / τ))
t += τ
ExtendableFEM.solve(PD, FES, SC; time = t)
end
end
# plot final state
plot!(plt, [id(u)], sol; keep = 1, title_add = " (t = $T)")
return sol, plt
end
end # moduleThis page was generated using Literate.jl.