250 : Navier–Stokes Lid-driven cavity
This example computes the velocity $\mathbf{u}$ and pressure $\mathbf{p}$ of the incompressible Navier–Stokes problem
\[\begin{aligned} - \mu \Delta \mathbf{u} + \left(\mathbf{u} \cdot \nabla\right) \mathbf{u}+ \nabla p & = \mathbf{f}\\ \mathrm{div}(\mathbf{u}) & = 0 \end{aligned}\]
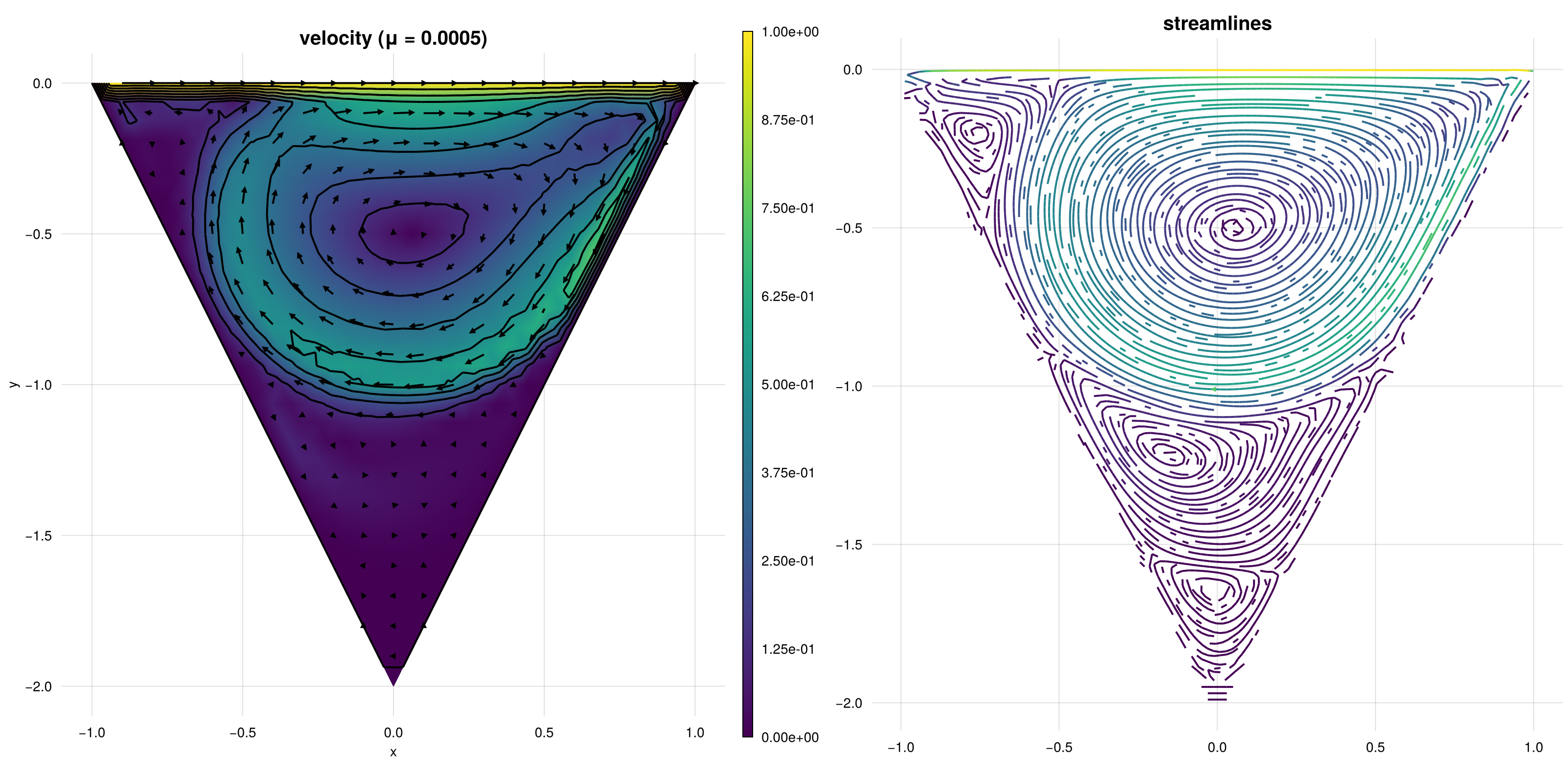
in a lid driven cavity example over a cone and plots the solution and the formed eddies.
The computed solution for the default parameters looks like this:
module Example250_NSELidDrivenCavity
using ExtendableFEM
using GridVisualize
using ExtendableGrids
using LinearAlgebra
function kernel_nonlinear!(result, u_ops, qpinfo)
u, ∇u, p = view(u_ops, 1:2), view(u_ops, 3:6), view(u_ops, 7)
μ = qpinfo.params[1]
result[1] = dot(u, view(∇u, 1:2))
result[2] = dot(u, view(∇u, 3:4))
result[3] = μ * ∇u[1] - p[1]
result[4] = μ * ∇u[2]
result[5] = μ * ∇u[3]
result[6] = μ * ∇u[4] - p[1]
result[7] = -(∇u[1] + ∇u[4])
return nothing
end
function boundarydata!(result, qpinfo)
result[1] = 1
result[2] = 0
end
function initialgrid_cone()
xgrid = ExtendableGrid{Float64, Int32}()
xgrid[Coordinates] = Array{Float64, 2}([-1 0; 0 -2; 1 0]')
xgrid[CellNodes] = Array{Int32, 2}([1 2 3]')
xgrid[CellGeometries] = VectorOfConstants{ElementGeometries, Int}(Triangle2D, 1)
xgrid[CellRegions] = ones(Int32, 1)
xgrid[BFaceRegions] = Array{Int32, 1}([1, 2, 3])
xgrid[BFaceNodes] = Array{Int32, 2}([1 2; 2 3; 3 1]')
xgrid[BFaceGeometries] = VectorOfConstants{ElementGeometries, Int}(Edge1D, 3)
xgrid[CoordinateSystem] = Cartesian2D
return xgrid
end
function main(; μ_final = 0.0005, order = 2, nrefs = 5, Plotter = nothing, kwargs...)
# prepare parameter field
extra_params = Array{Float64, 1}([max(μ_final, 0.05)])
# problem description
PD = ProblemDescription()
u = Unknown("u"; name = "velocity")
p = Unknown("p"; name = "pressure")
assign_unknown!(PD, u)
assign_unknown!(PD, p)
assign_operator!(PD, NonlinearOperator(kernel_nonlinear!, [id(u), grad(u), id(p)]; params = extra_params, kwargs...))
assign_operator!(PD, InterpolateBoundaryData(u, boundarydata!; regions = 3))
assign_operator!(PD, HomogeneousBoundaryData(u; regions = [1, 2]))
assign_operator!(PD, FixDofs(p; dofs = [1]))
# grid
xgrid = uniform_refine(initialgrid_cone(), nrefs)
# prepare FESpace
FES = [FESpace{H1Pk{2,2,order}}(xgrid), FESpace{H1Pk{1,2,order-1}}(xgrid)]
# prepare plots
plt = GridVisualizer(; Plotter = Plotter, layout = (1, 2), clear = true, size = (1600, 800))
# solve by μ embedding
step = 0
sol = nothing
SC = nothing
PE = PointEvaluator([id(1)])
while (true)
step += 1
@info "Step $step : solving for μ=$(extra_params[1])"
sol, SC = ExtendableFEM.solve(PD, FES, SC; return_config = true, target_residual = 1e-10, maxiterations = 20, kwargs...)
if step == 1
initialize!(PE, sol)
end
scalarplot!(plt[1, 1], xgrid, nodevalues(sol[1]; abs = true)[1, :]; title = "velocity (μ = $(extra_params[1]))", Plotter = Plotter)
vectorplot!(plt[1, 1], xgrid, eval_func_bary(PE), spacing = 0.05, clear = false)
streamplot!(plt[1, 2], xgrid, eval_func_bary(PE), spacing = 0.01, density = 2, title = "streamlines")
if extra_params[1] <= μ_final
break
else
extra_params[1] = max(μ_final, extra_params[1] / 2)
end
end
scalarplot!(plt[1, 1], xgrid, nodevalues(sol[1]; abs = true)[1, :]; title = "velocity (μ = $(extra_params[1]))", Plotter = Plotter)
vectorplot!(plt[1, 1], xgrid, eval_func_bary(PE), spacing = 0.05, clear = false)
streamplot!(plt[1, 2], xgrid, eval_func_bary(PE), spacing = 0.01, density = 2, title = "streamlines")
return sol, plt
end
end # moduleThis page was generated using Literate.jl.