204 : Eigenvalue problem for the Laplacian
This example computes the pairs of eigenvalues and eigenvectors $(\lambda,u) \in \mathbb{R} \times H^1_0(\Omega)$ of the Laplacian, i.e,
\[\begin{aligned} -\Delta u & = \lambda u \quad \text{in } \Omega \end{aligned}\]
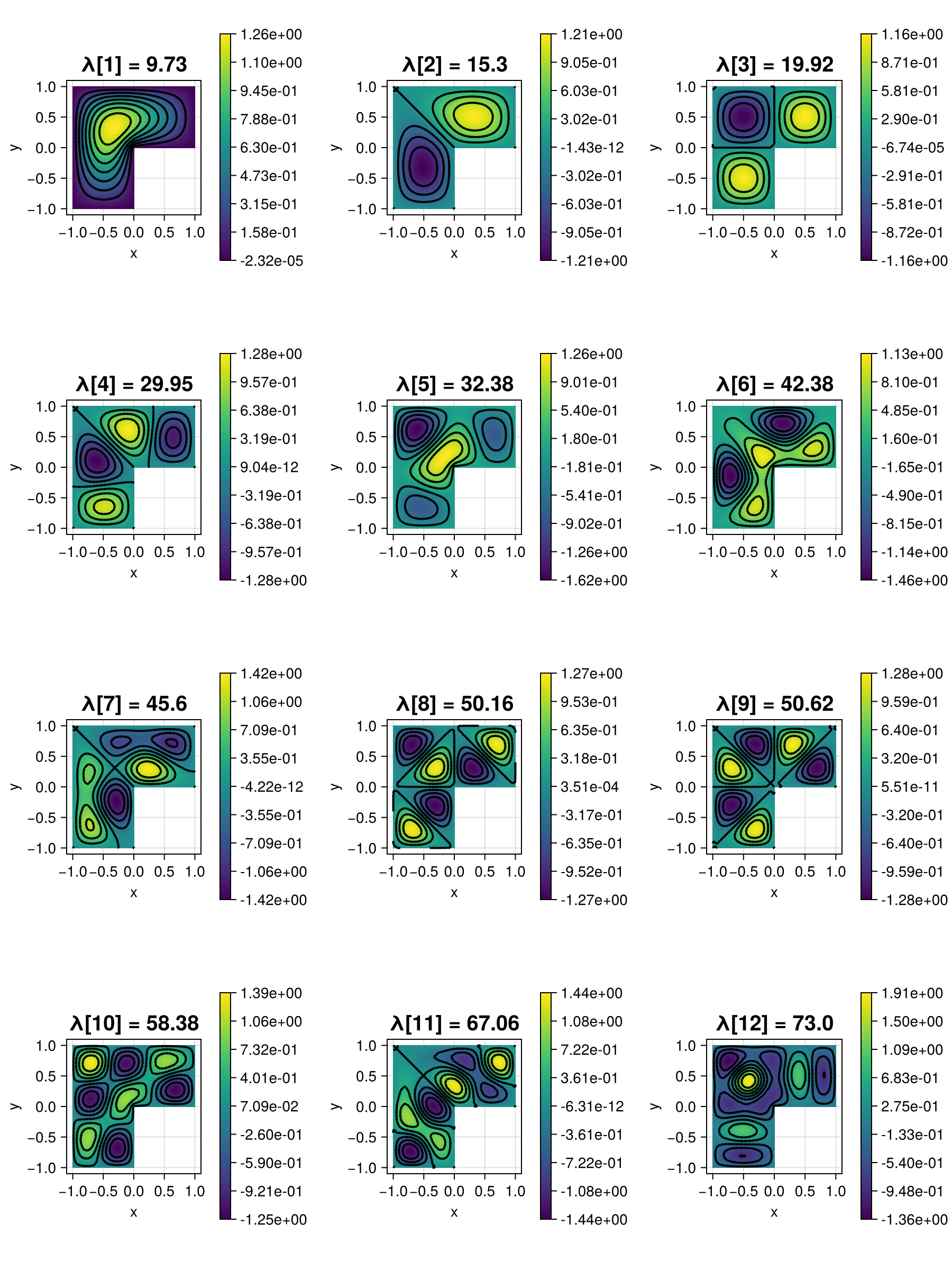
on a two-dimensional L-shaped domain with homogeneous boundary conditions with the help of an iterative solver from KrylovKit.jl. The first twelve computed eigenvectors look like this:
module Example204_LaplaceEVProblem
using ExtendableFEM
using ExtendableGrids
using ExtendableSparse
using LinearAlgebra
using GridVisualize
using KrylovKit
function main(; which = 1:12, ncols = 3, nrefs = 4, order = 1, Plotter = nothing, kwargs...)
# discretize
xgrid = uniform_refine(grid_lshape(Triangle2D), nrefs)
FES = FESpace{H1Pk{1, 2, order}}(xgrid)
# assemble operators
A = FEMatrix(FES)
B = FEMatrix(FES)
u = FEVector(FES; name = "u")
assemble!(A, BilinearOperator([grad(1)]; kwargs...))
assemble!(A, BilinearOperator([id(1)]; entities = ON_BFACES, factor = 1e4, kwargs...))
assemble!(B, BilinearOperator([id(1)]; kwargs...))
# solver generalized eigenvalue problem iteratively with KrylovKit
λs, x, info = geneigsolve((A.entries, B.entries), maximum(which), :SR; maxiter = 4000, issymmetric = true, tol = 1e-8)
@show info
@assert info.converged >= maximum(which)
# plot requested eigenvalue pairs
nEVs = length(which)
nrows = Int(ceil(nEVs / ncols))
plt = GridVisualizer(; Plotter = Plotter, layout = (nrows, ncols), clear = true, resolution = (900, 900 / ncols * nrows))
col, row = 0, 1
for j in which
col += 1
if col == ncols + 1
col, row = 1, row + 1
end
λ = λs[j]
@info "λ[$j] = $λ, residual = $(sum(info.residual[j]))"
u.entries .= Real.(x[j])
scalarplot!(plt[row, col], id(1), u; Plotter = Plotter, title = "λ[$j] = $(Float16(λ))")
end
return u, plt
end
end # moduleThis page was generated using Literate.jl.