240 : Stokes $RT$ enrichment
This example computes the velocity $\mathbf{u}$ and pressure $\mathbf{p}$ of the incompressible Stokes problem
\[\begin{aligned} - \mu \Delta \mathbf{u} + \nabla p & = \mathbf{f}\\ \mathrm{div}(\mathbf{u}) & = 0 \end{aligned}\]
with exterior force $\mathbf{f}$ and some parameter $\mu$ and inhomogeneous Dirichlet boundary data.
The problem will be solved by a $(P_k \oplus RTenrichment) \times P_{k-1}$ scheme, which can be seen as an inf-sup stabilized Scott-Vogelius variant that works with general meshes, see references below. Therein, the velocity space employs continuous $P_{k}$ functions plus certain (only H(div)-conforming) Raviart-Thomas functions and a discontinuous $P_{k-1}$ pressure space leading to an exactly divergence-free discrete velocity. In a reduction step (that can be triggered with the reduce switch) all higher order pressure dofs and the enrichment dofs can be eliminated from the system.
"A low-order divergence-free H(div)-conforming finite element method for Stokes flows",
X. Li, H. Rui,
IMA Journal of Numerical Analysis (2021),
>Journal-Link< >Preprint-Link<
"Inf-sup stabilized Scott–Vogelius pairs on general simplicial grids by Raviart–Thomas enrichment",
V. John, X. Li, C. Merdon, H. Rui,
>Preprint-Link<
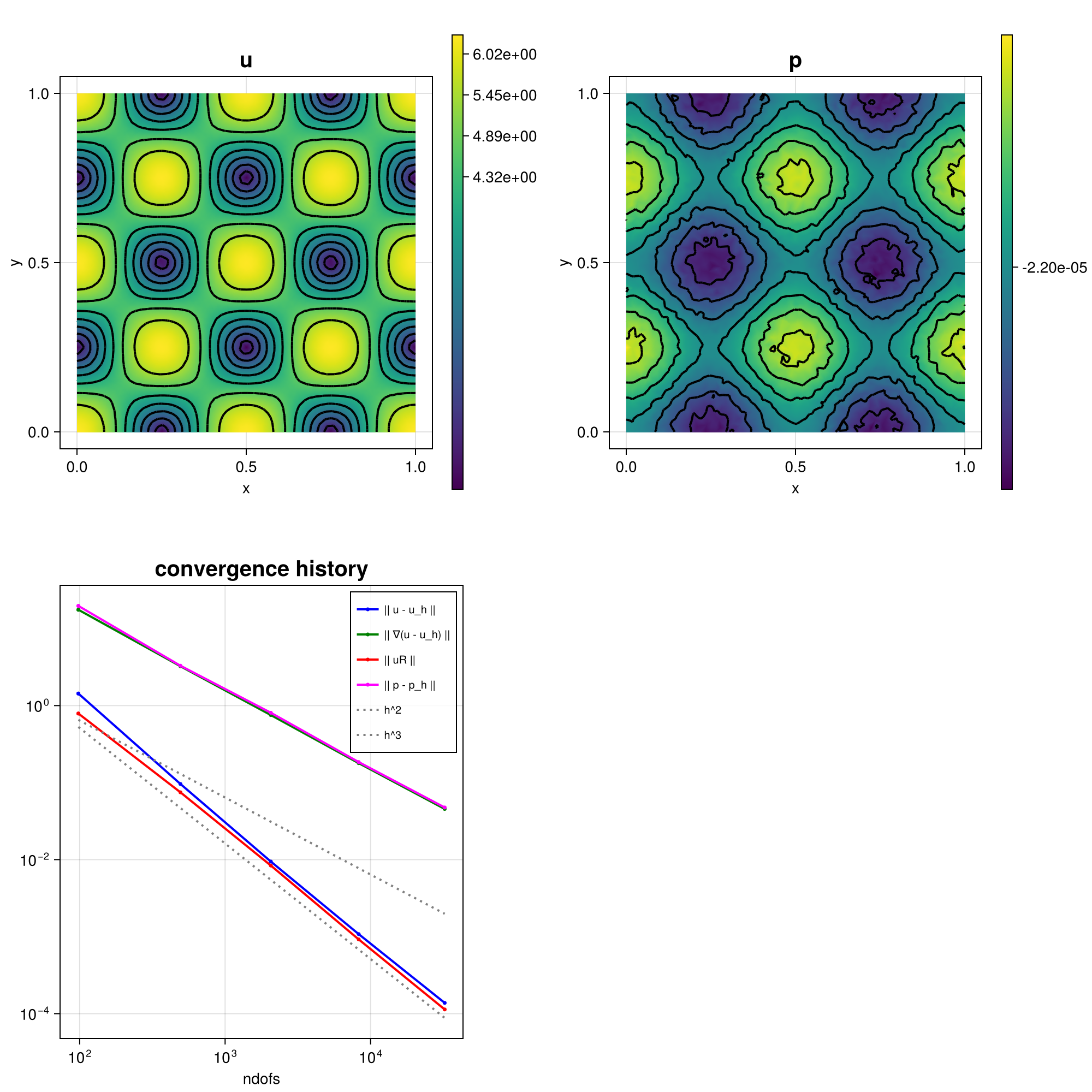
The computed solution for the default parameters looks like this:
module Example240_SVRTEnrichment
using ExtendableFEM
using GridVisualize
using ExtendableGrids
using ExtendableSparse
using Triangulate
using SimplexGridFactory
using Symbolics
# exact data for problem generated by Symbolics
function prepare_data(; μ = 1)
@variables x y
# stream function ξ
ξ = -sin(2 * pi * x) * cos(2 * pi * y)
# velocity u = curl ξ
∇ξ = Symbolics.gradient(ξ, [x, y])
u = [-∇ξ[2], ∇ξ[1]]
# pressure
p = (cos(4 * pi * x) - cos(4 * pi * y)) / 4
# gradient of velocity
∇u = Symbolics.jacobian(u, [x, y])
∇u_reshaped = [∇u[1, 1], ∇u[1, 2], ∇u[2, 1], ∇u[2, 2]]
# Laplacian
Δu = [
(Symbolics.gradient(∇u[1, 1], [x])+Symbolics.gradient(∇u[1, 2], [y]))[1],
(Symbolics.gradient(∇u[2, 1], [x])+Symbolics.gradient(∇u[2, 2], [y]))[1],
]
# right-hand side
f = -μ * Δu + Symbolics.gradient(p, [x, y])
# build functions
p_eval = build_function(p, x, y, expression = Val{false})
u_eval = build_function(u, x, y, expression = Val{false})
∇u_eval = build_function(∇u_reshaped, x, y, expression = Val{false})
f_eval = build_function(f, x, y, expression = Val{false})
return f_eval[2], u_eval[2], ∇u_eval[2], p_eval
end
# grid generator function
function get_grid2D(nref; uniform = false, barycentric = false)
if uniform || barycentric
gen_ref = 0
else
gen_ref = nref
end
grid = simplexgrid(Triangulate;
points = [0 0; 0 1; 1 1; 1 0]',
bfaces = [1 2; 2 3; 3 4; 4 1]',
bfaceregions = [1, 2, 3, 4],
regionpoints = [0.5 0.5;]',
regionnumbers = [1],
regionvolumes = [4.0^(-gen_ref - 1)])
if uniform
grid = uniform_refine(grid, nref)
end
if barycentric
grid = barycentric_refine(grid)
end
return grid
end
# kernel for Stokes operator
function kernel_stokes_standard!(result, u_ops, qpinfo)
∇u, p = view(u_ops, 1:4), view(u_ops, 5)
μ = qpinfo.params[1]
result[1] = μ * ∇u[1] - p[1]
result[2] = μ * ∇u[2]
result[3] = μ * ∇u[3]
result[4] = μ * ∇u[4] - p[1]
result[5] = -(∇u[1] + ∇u[4])
return nothing
end
function main(; nrefs = 5, μ = 1, α = 1, order = 2, Plotter = nothing, enrich = true, reduce = true, time = 0.5, bonus_quadorder = 5, kwargs...)
# prepare problem data
f_eval, u_eval, ∇u_eval, p_eval = prepare_data(; μ = μ)
rhs!(result, qpinfo) = (f_eval(result, qpinfo.x[1], qpinfo.x[2]))
exact_p!(result, qpinfo) = (result[1] = p_eval(qpinfo.x[1], qpinfo.x[2]))
exact_u!(result, qpinfo) = (u_eval(result, qpinfo.x[1], qpinfo.x[2]))
exact_∇u!(result, qpinfo) = (∇u_eval(result, qpinfo.x[1], qpinfo.x[2]))
# prepare unknowns
u = Unknown("u"; name = "velocity", dim = 2)
pfull = Unknown("p"; name = "pressure (full)", dim = 1)
pE = Unknown("p⟂"; name = "pressure (enriched)", dim = 1)
p0 = Unknown("p0"; name = "pressure (reduced)", dim = 1) # only used if enrich && reduced
uR = Unknown("uR"; name = "velocity enrichment", dim = 2) # only used if enrich == true
# prepare plots
plt = GridVisualizer(; Plotter = Plotter, layout = (2, 2), clear = true, size = (1000, 1000))
# prepare error calculations
function exact_error!(result, u, qpinfo)
exact_u!(view(result, 1:2), qpinfo)
exact_∇u!(view(result, 3:6), qpinfo)
result .-= u
result .= result .^ 2
end
function exact_error_p!(result, p, qpinfo)
exact_p!(view(result, 1), qpinfo)
result .-= p
result .= result .^ 2
end
ErrorIntegratorExact = ItemIntegrator(exact_error!, [id(u), grad(u)]; quadorder = 2 * (order + 1), kwargs...)
ErrorIntegratorPressure = ItemIntegrator(exact_error_p!, [order == 1 ? id(p0) : id(pfull)]; quadorder = 2 * (order + 1), kwargs...)
L2NormIntegratorE = L2NormIntegrator([id(uR)]; quadorder = 2 * order)
function kernel_div!(result, u, qpinfo)
result .= sum(u) .^ 2
end
DivNormIntegrator = ItemIntegrator(kernel_div!, enrich ? [div(u), div(uR)] : [div(u)]; quadorder = 2 * order)
NDofs = zeros(Int, nrefs)
Results = zeros(Float64, nrefs, 5)
for lvl ∈ 1:nrefs
# grid
xgrid = get_grid2D(lvl)
# define and assign unknowns
PD = ProblemDescription("Stokes problem")
assign_unknown!(PD, u)
p = reduce * enrich ? p0 : pfull
assign_unknown!(PD, p)
################
### FESPACES ###
################
if order == 1
FES_enrich = FESpace{HDIVRT0{2}}(xgrid)
else
FES_enrich = FESpace{HDIVRTkENRICH{2, order - 1, reduce}}(xgrid)
end
FES = Dict(u => FESpace{H1Pk{2, 2, order}}(xgrid),
pfull => FESpace{order == 1 ? L2P0{1} : H1Pk{1, 2, order - 1}}(xgrid; broken = true),
p0 => FESpace{L2P0{1}}(xgrid; broken = true),
uR => enrich ? FES_enrich : nothing)
######################
### STANDARD TERMS ###
######################
assign_operator!(PD, LinearOperator(rhs!, [id(u)]; bonus_quadorder = bonus_quadorder, kwargs...))
assign_operator!(PD, BilinearOperator(kernel_stokes_standard!, [grad(u), id(p)]; params = [μ], kwargs...))
assign_operator!(PD, InterpolateBoundaryData(u, exact_u!; regions = 1:4, bonus_quadorder = bonus_quadorder))
assign_operator!(PD, FixDofs(p; dofs = [1], vals = [0]))
##################
### ENRICHMENT ###
##################
if enrich
if reduce
if order == 1
@info "... preparing condensation of RT0 dofs"
AR = FEMatrix(FES_enrich)
BR = FEMatrix(FES[p], FES_enrich)
bR = FEVector(FES_enrich)
assemble!(AR, BilinearOperator([div(1)]; lump = true, factor = α*μ, kwargs...))
for bface in xgrid[BFaceFaces]
AR.entries[bface, bface] = 1e60
end
assemble!(BR, BilinearOperator([id(1)], [div(1)]; factor = -1, kwargs...))
assemble!(bR, LinearOperator(rhs!, [id(1)]; bonus_quadorder = 5, kwargs...); time = time)
# invert AR (diagonal matrix)
AR.entries.cscmatrix.nzval .= 1 ./ AR.entries.cscmatrix.nzval
C = -BR.entries.cscmatrix * AR.entries.cscmatrix * BR.entries.cscmatrix'
c = -BR.entries.cscmatrix * AR.entries.cscmatrix * bR.entries
assign_operator!(PD, BilinearOperator(C, [p], [p]; kwargs...))
assign_operator!(PD, LinearOperator(c, [p]; kwargs...))
else
@info "... preparing removal of enrichment dofs"
BR = FEMatrix(FES[p], FES_enrich)
A1R = FEMatrix(FES_enrich, FES[u])
bR = FEVector(FES_enrich)
assemble!(BR, BilinearOperator([id(1)], [div(1)]; factor = -1, kwargs...))
assemble!(bR, LinearOperator(rhs!, [id(1)]; bonus_quadorder = 5, kwargs...); time = time)
assemble!(A1R, BilinearOperator([id(1)], [Δ(1)]; factor = -μ, kwargs...))
F, DD_RR = div_projector(FES[u], FES_enrich)
C = F.entries.cscmatrix * A1R.entries.cscmatrix
assign_operator!(PD, BilinearOperator(C, [u], [u]; factor = 1, transposed_copy = -1, kwargs...))
assign_operator!(PD, LinearOperator(F.entries.cscmatrix * bR.entries, [u]; kwargs...))
end
else
assign_unknown!(PD, uR)
assign_operator!(PD, LinearOperator(rhs!, [id(uR)]; bonus_quadorder = 5, kwargs...))
assign_operator!(PD, BilinearOperator([id(p)], [div(uR)]; transposed_copy = 1, factor = -1, kwargs...))
if order == 1
assign_operator!(PD, BilinearOperator([div(uR)]; lump = true, factor = μ, kwargs...))
assign_operator!(PD, HomogeneousBoundaryData(uR; regions = 1:4))
else
assign_operator!(PD, BilinearOperator([Δ(u)], [id(uR)]; factor = μ, transposed_copy = -1, kwargs...))
end
end
end
#############
### SOLVE ###
#############
sol = solve(PD, FES; time = time, kwargs...)
NDofs[lvl] = length(sol.entries)
# move integral mean of pressure
pintegrate = ItemIntegrator([id(p)])
pmean = sum(evaluate(pintegrate, sol)) / sum(xgrid[CellVolumes])
view(sol[p]) .-= pmean
######################
### POSTPROCESSING ###
######################
if enrich && reduce
append!(sol, FES_enrich; tag = uR)
if order == 1
# compute enrichment part of velocity
view(sol[uR]) .= AR.entries.cscmatrix * (bR.entries - BR.entries.cscmatrix' * view(sol[p]))
else
# compute enrichment part of velocity
view(sol[uR]) .= F.entries.cscmatrix' * view(sol[u])
end
# compute higher order pressure dofs
if reduce && order > 1
# add blocks for higher order pressures to sol vector
VR = FES_enrich
append!(sol, VR; tag = pE)
append!(sol, FES[pfull]; tag = pfull)
sol_pE = view(sol[pE])
sol_pfull = view(sol[pfull])
sol_p0 = view(sol[p0])
res = FEVector(VR)
addblock_matmul!(res[1], A1R[1, 1], sol[u])
celldofs_VR::VariableTargetAdjacency{Int32} = VR[CellDofs]
ndofs_VR = max_num_targets_per_source(celldofs_VR)
Ap = zeros(Float64, ndofs_VR, ndofs_VR)
bp = zeros(Float64, ndofs_VR)
xp = zeros(Float64, ndofs_VR)
for cell ∈ 1:num_cells(xgrid)
# solve local pressure reconstruction
# (p_h, div VR) = - (f,VR) + a_h(u_h,VR)
for dof_j ∈ 1:ndofs_VR
dof = celldofs_VR[dof_j, cell]
bp[dof_j] = -bR.entries[dof] + res.entries[dof]
for dof_k ∈ 1:ndofs_VR
dof2 = celldofs_VR[dof_k, cell]
Ap[dof_j, dof_k] = DD_RR.entries[dof, dof2]
end
end
# solve for coefficients of div(RT1bubbles)
xp = Ap \ bp
# save in block id_pk
for dof_j ∈ 1:ndofs_VR
dof = celldofs_VR[dof_j, cell]
sol_pE[dof] = xp[dof_j]
end
end
# interpolate into Pk basis (= same pressure basis as in full scheme)
PF = FES[pfull]
append!(sol, PF; tag = pfull)
celldofs_PF::SerialVariableTargetAdjacency{Int32} = PF[CellDofs]
ndofs_PF::Int = max_num_targets_per_source(celldofs_PF)
# compute local mass matrix of full pressure space
MAMA = FEMatrix(PF)
assemble!(MAMA, BilinearOperator([id(1)]))
MAMAE::ExtendableSparseMatrix{Float64, Int64} = MAMA.entries
# full div-pressure matrix
PFxVR = FEMatrix(PF, VR)
assemble!(PFxVR, BilinearOperator([id(1)], [div(1)]))
PFxVRE::ExtendableSparseMatrix{Float64, Int64} = PFxVR.entries
bp = zeros(Float64, ndofs_PF)
xp = zeros(Float64, ndofs_PF)
locMAMA = zeros(Float64, ndofs_PF, ndofs_PF)
for cell ∈ 1:num_cells(xgrid)
# solve local pressure reconstruction
fill!(bp, 0)
for dof_k ∈ 1:ndofs_PF
dof2 = celldofs_PF[dof_k, cell]
for dof_j ∈ 1:ndofs_VR
dof = celldofs_VR[dof_j, cell]
bp[dof_k] += PFxVRE[dof2, dof] * sol_pE[dof]
end
for dof_j ∈ 1:ndofs_PF
dof = celldofs_PF[dof_j, cell]
locMAMA[dof_k, dof_j] = MAMAE[dof2, dof]
end
end
# solve for coefficients of div(RT1bubbles)
xp = locMAMA \ bp
for dof_j ∈ 1:ndofs_PF
dof = celldofs_PF[dof_j, cell]
sol_pfull[dof] = sol_p0[cell] + xp[dof_j]
end
end
elseif reduce && order == 1
pfull = p0
end
end
########################
### ERROR EVALUATION ###
########################
error = evaluate(ErrorIntegratorExact, sol)
L2errorU = sqrt(sum(view(error, 1, :)) + sum(view(error, 2, :)))
H1errorU = sqrt(sum(view(error, 3, :)) + sum(view(error, 4, :)) + sum(view(error, 5, :)) + sum(view(error, 6, :)))
@info "L2error(u) = $L2errorU"
@info "L2error(∇u) = $H1errorU"
evaluate!(error, ErrorIntegratorPressure, sol)
L2errorP = sqrt(sum(view(error, 1, :)))
@info "L2error(p) = $L2errorP"
Results[lvl, 4] = L2errorP
if enrich
fill!(error, 0)
evaluate!(error, L2NormIntegratorE, sol)
L2normUR = sqrt(sum(view(error, 1, :)) + sum(view(error, 2, :)))
@info "L2norm(uR) = $L2normUR"
end
fill!(error, 0)
evaluate!(error, DivNormIntegrator, sol)
L2normDiv = sqrt(sum(view(error, 1, :)))
@info "L2norm(div(u+uR)) = $L2normDiv"
Results[lvl, 1] = L2errorU
Results[lvl, 2] = H1errorU
Results[lvl, 3] = L2normUR
Results[lvl, 5] = L2normDiv
#############
### PLOTS ###
#############
scalarplot!(plt[1, 1], id(u), sol; abs = true)
scalarplot!(plt[1, 2], id(pfull), sol)
if order == 1 && enrich
scalarplot!(plt[2, 2], id(uR), sol)
end
end
plot_convergencehistory!(
plt[2, 1],
NDofs,
Results[:,1:4];
add_h_powers = [order, order + 1],
X_to_h = X -> 8 * X .^ (-1 / 2),
legend = :best,
ylabels = ["|| u - u_h ||", "|| ∇(u - u_h) ||", "|| uR ||", "|| p - p_h ||", "|| div(u + uR) ||"],
)
print_convergencehistory(NDofs, Results; X_to_h = X -> X .^ (-1 / 2), ylabels = ["|| u - u_h ||", "|| ∇(u - u_h) ||", "|| uR ||", "|| p - p_h ||", "|| div(u + uR) ||"], xlabel = "ndof")
return Results, plt
end
function div_projector(V1, VR)
# setup interpolation matrix
celldofs_V1 = V1[CellDofs]
celldofs_VR = VR[CellDofs]
ndofs_V1 = max_num_targets_per_source(celldofs_V1)
ndofs_VR = max_num_targets_per_source(celldofs_VR)
DD_RR = FEMatrix(VR)
assemble!(DD_RR, BilinearOperator([div(1)]))
DD_RRE = DD_RR.entries
DD_1R = FEMatrix(V1, VR)
assemble!(DD_1R, BilinearOperator([div(1)]))
DD_1RE = DD_1R.entries
Ap = zeros(Float64, ndofs_VR, ndofs_VR)
bp = zeros(Float64, ndofs_VR)
xp = zeros(Float64, ndofs_VR)
ncells = num_sources(celldofs_V1)
F = FEMatrix(V1, VR)
FE = F.entries
for cell ∈ 1:ncells
# solve local pressure reconstruction for RTk part
for dof_j ∈ 1:ndofs_VR
dof = celldofs_VR[dof_j, cell]
for dof_k ∈ 1:ndofs_VR
dof2 = celldofs_VR[dof_k, cell]
Ap[dof_j, dof_k] = DD_RRE[dof, dof2]
end
end
for dof_j ∈ 1:ndofs_V1
dof = celldofs_V1[dof_j, cell]
for dof_k ∈ 1:ndofs_VR
dof2 = celldofs_VR[dof_k, cell]
bp[dof_k] = -DD_1RE[dof, dof2]
end
xp = Ap \ bp
for dof_k ∈ 1:ndofs_VR
dof2 = celldofs_VR[dof_k, cell]
FE[dof, dof2] = xp[dof_k]
end
end
end
flush!(FE)
return F, DD_RR
end
end # moduleThis page was generated using Literate.jl.