245 : Flow around a cylinder
This example solves the DFG Navier-Stokes benchmark problem
\[\begin{aligned} - \mu \Delta \mathbf{u} + (\mathbf{u} \cdot \nabla) \mathbf{u} + \nabla p & = 0\\ \mathrm{div}(\mathbf{u}) & = 0 \end{aligned}\]
on a rectangular 2D domain with a circular obstacle, see here for details.
This script demonstrates the employment of external grid generators and the computation of drag and lift coefficients.
Note: This example needs the additional packages Triangulate and SimplexGridFactory to generate the mesh.
module Example245_NSEFlowAroundCylinder
using ExtendableFEM
using Triangulate
using SimplexGridFactory
using ExtendableGrids
using GridVisualize
using LinearAlgebra
# inlet data for Karman vortex street example
# as in DFG benchmark 2D-1 (Re = 20, laminar)
const umax = 0.3
const umean = 2 // 3 * umax
const L, W, H = 0.1, 2.2, 0.41
function inflow!(result, qpinfo)
x = qpinfo.x
result[1] = 4 * umax * x[2] * (H - x[2]) / (H * H)
result[2] = 0.0
end
# hand constructed identity matrix for kernel to avoid allocations
const II = [1 0; 0 1]
# Example of a kernel using tensor_view() function to allow for an operator
# based style of writing the semilinear form.
# For comparison we also provide the kernel_nonlinear_flat! function below
# that uses a component-wise style of writing the semilinear form.
#
# the scalar product ``(\nabla v, \mu \nabla u - p)`` will be evaluated
# so in general `a = b` corresponds to ``(a,b)``.
# Note that the order of vector entries between the kernel and the call to
# NonlinearOperator have to match.
function kernel_nonlinear!(result, u_ops, qpinfo)Shape values of vectorial u are starting at index 1 view as 1-tensor(vector) of length dim=2 in 2D
u = tensor_view(u_ops, 1, TDVector(2))
v = tensor_view(result, 1, TDVector(2))gradients of vectorial u are starting at index 3 view as 2-tensor of size 2x2 in 2D
∇u = tensor_view(u_ops, 3, TDMatrix(2))
∇v = tensor_view(result, 3, TDMatrix(2))values of scalar p are starting at index 7 view as 0-tensor (single value)
p = tensor_view(u_ops, 7, TDScalar())
q = tensor_view(result, 7, TDScalar())get viscosity at current quadrature point
μ = qpinfo.params[1]Note that all operators should be element-wise to avoid allocations (v,u⋅∇u) = (v,∇u^T⋅u)
tmul!(v,∇u,u)(∇v,μ∇u-p)
∇v .= μ .* ∇u .- p[1] .* II(q,-∇⋅u)
q[1] = -dot(∇u, II)
return nothing
end
# everything is wrapped in a main function
function main(; Plotter = nothing, μ = 1e-3, maxvol = 1e-3, reconstruct = true, kwargs...)
# load grid (see function below)
xgrid = make_grid(W, H; n = Int(ceil(sqrt(1 / maxvol))), maxvol = maxvol)
# problem description
PD = ProblemDescription()
u = Unknown("u"; name = "velocity")
p = Unknown("p"; name = "pressure")
id_u = reconstruct ? apply(u, Reconstruct{HDIVRT1{2}, Identity}) : id(u)
assign_unknown!(PD, u)
assign_unknown!(PD, p)
assign_operator!(PD, NonlinearOperator(kernel_nonlinear!, [id_u, grad(u), id(p)]; params = [μ], kwargs...))
assign_operator!(PD, InterpolateBoundaryData(u, inflow!; regions = 4))
assign_operator!(PD, HomogeneousBoundaryData(u; regions = [1, 3, 5]))
# P2-bubble + reconstruction operator
FETypes = [H1P2B{2, 2}, H1P1{1}]
# generate FESpaces and Solution vector
FES = [FESpace{FETypes[1]}(xgrid), FESpace{FETypes[2]}(xgrid; broken = true)]
# solve
sol = solve(PD, FES; maxiterations = 50, target_residual = 1e-10)
# postprocess : compute drag/lift (see function below)
draglift = get_draglift(sol, μ)
pdiff = get_pressure_difference(sol)
println("[drag, lift] = $draglift")
println("p difference = $pdiff")
# plots via GridVisualize
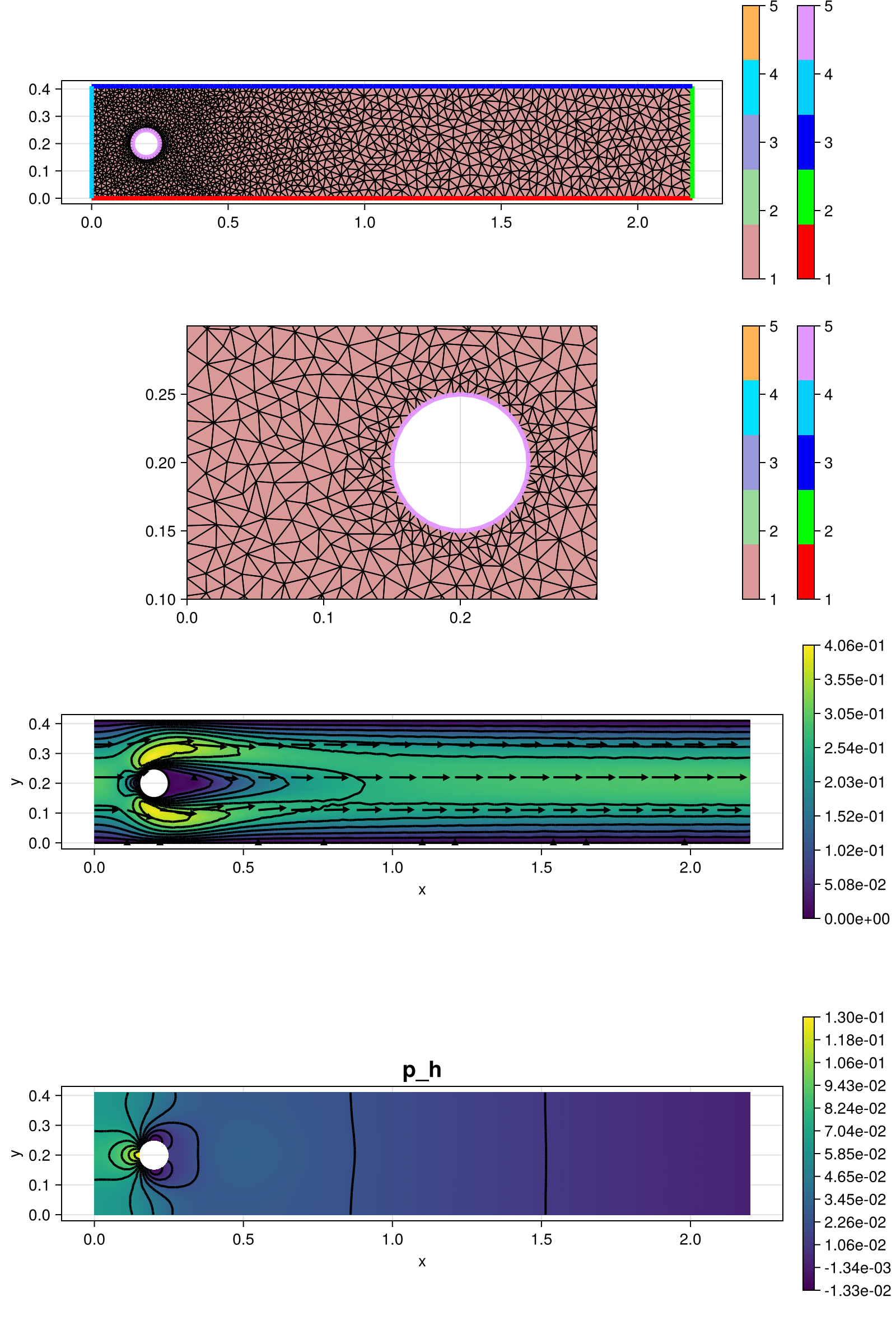
plt = GridVisualizer(; Plotter = Plotter, layout = (4, 1), clear = true, size = (800, 1200))
gridplot!(plt[1, 1], xgrid, linewidth = 1)
gridplot!(plt[2, 1], xgrid, linewidth = 1, xlimits = [0, 0.3], ylimits = [0.1, 0.3])
scalarplot!(plt[3, 1], xgrid, nodevalues(sol[u]; abs = true)[1, :])
vectorplot!(plt[3, 1], xgrid, eval_func_bary(PointEvaluator([id(u)], sol)), spacing = (0.2, 0.05), vscale = 0.5, clear = false)
scalarplot!(plt[4, 1], xgrid, view(nodevalues(sol[p]), 1, :), levels = 11, title = "p_h")
return [draglift[1], draglift[2], pdiff[1]], plt
end
function get_pressure_difference(sol::FEVector)
xgrid = sol[2].FES.xgrid
PE = PointEvaluator([id(2)], sol)
p_left = zeros(Float64, 1)
x1 = [0.15, 0.2]
p_right = zeros(Float64, 1)
x2 = [0.25, 0.2]
evaluate!(p_left, PE, x1)
evaluate!(p_right, PE, x2)
@show p_left, p_right
return p_left - p_right
end
function get_draglift(sol::FEVector, μ)
# this function is interpolated for drag/lift test function creation
function DL_testfunction(component)
function closure(result, qpinfo)
x = qpinfo.x
fill!(result, 0)
if sqrt((x[1] - 0.2)^2 + (x[2] - 0.2)^2) <= 0.06
result[component] = 1
end
end
end
# drag lift calcuation by testfunctions
function draglift_kernel(result, input, qpinfo)
# input = [ u, grad(u), p , v , grad(v)]
# [1:2, 3:6, 7 ,8:9, 10:13 ]
result[1] = μ * (input[3] * input[10] + input[4] * input[11] + input[5] * input[12] + input[6] * input[13])
result[1] += (input[1] * input[3] + input[2] * input[4]) * input[8]
result[1] += (input[1] * input[5] + input[2] * input[6]) * input[9]
result[1] -= input[7] * (input[10] + input[13])
result[1] *= -(2 / (umean^2 * L))
return nothing
end
DLIntegrator = ItemIntegrator(draglift_kernel, [id(1), grad(1), id(2), id(3), grad(3)]; quadorder = 4)
# test for drag
TestFunction = FEVector(sol[1].FES; name = "drag/lift testfunction")
interpolate!(TestFunction[1], ON_BFACES, DL_testfunction(1))
drag = sum(evaluate(DLIntegrator, [sol[1], sol[2], TestFunction[1]]))
# test for lift
interpolate!(TestFunction[1], ON_BFACES, DL_testfunction(2))
lift = sum(evaluate(DLIntegrator, [sol[1], sol[2], TestFunction[1]]))
return [drag, lift]
end
# grid generator script using SimplexGridBuilder/Triangulate
function make_grid(W, H; n = 20, maxvol = 0.1)
builder = SimplexGridBuilder(Generator = Triangulate)
function circlehole!(builder, center, radius; n = 20)
points = [point!(builder, center[1] + radius * sin(t), center[2] + radius * cos(t)) for t in range(0, 2π, length = n)]
for i ∈ 1:n-1
facet!(builder, points[i], points[i+1])
end
facet!(builder, points[end], points[1])
holepoint!(builder, center)
end
p1 = point!(builder, 0, 0)
p2 = point!(builder, W, 0)
p3 = point!(builder, W, H)
p4 = point!(builder, 0, H)
# heuristic refinement around cylinder
refine_radius = 0.25
maxrefinefactor = 1 // 20
function unsuitable(x1, y1, x2, y2, x3, y3, area)
if area > maxvol * min(max(4 * maxrefinefactor, abs((x1 + x2 + x3) / 3 - 0.2)), 1 / maxrefinefactor)
return true
end
dist = sqrt(((x1 + x2 + x3) / 3 - 0.2)^2 + ((y1 + y2 + y3) / 3 - 0.2)^2) - 0.05
myarea = dist < refine_radius ? maxvol * max(maxrefinefactor, 1 - (refine_radius - dist) / refine_radius) : maxvol
if area > myarea
return true
else
return false
end
end
facetregion!(builder, 1)
facet!(builder, p1, p2)
facetregion!(builder, 2)
facet!(builder, p2, p3)
facetregion!(builder, 3)
facet!(builder, p3, p4)
facetregion!(builder, 4)
facet!(builder, p4, p1)
facetregion!(builder, 5)
circlehole!(builder, (0.2, 0.2), 0.05, n = n)
simplexgrid(builder, maxvolume = 16 * maxvol, unsuitable = unsuitable)
end
endThis page was generated using Literate.jl.