A09 : Poisson-Problem with low level structures

(source code)

This example computes the solution $u$ of the Poisson problem

\[\begin{aligned} -\Delta u & = f \quad \text{in } \Omega \end{aligned}\]

with some right-hand side $f = 1$ on the unit square domain $\Omega$ on a given grid.

Here, the whole problem is assembled with low level, mid level and high level structures and runtime and allocations in each step are compared.

module ExampleA09_PoissonLowLevel

using GradientRobustMultiPhysics
using ExtendableGrids
using ExtendableSparse
using LinearAlgebra
using GridVisualize

const f = x -> 1
const fdata = DataFunction((result, x) -> (result[1] = f(x);), [1,2]; dependencies = "X")

# everything is wrapped in a main function
function main(; verbosity = 0, order = 2, μ = 1, nrefinements = 3, Plotter = nothing)

    # set log level
    set_verbosity(verbosity)

    # build/load any grid (here: a uniform-refined 2D unit square into triangles)
    xgrid = uniform_refine(grid_unitsquare(Triangle2D), nrefinements)
    @info "preparing face nodes"
    @time xgrid[FaceNodes]
    @info "preparing cell volumes"
    @time cellvolumes = xgrid[CellVolumes]

    # choose FE type
    FEType = H1Pk{1,2,order}

    # create FESpace and vector
    FES = FESpace{FEType}(xgrid)
    SolutionLow = FEVector(FES)
    SolutionMid = FEVector(FES)
    SolutionHigh = FEVector(FES)

    # do this here once
    @info "preparing celldofs"
    @time CellDofs::Adjacency{Int32} = FES[GradientRobustMultiPhysics.CellDofs]
    @info "preparing bfacedofs"
    @time BFaceDofs::Adjacency{Int32} = FES[GradientRobustMultiPhysics.BFaceDofs]

    @info "ndofs = $(length(SolutionLow.entries))"
    @time solve_poisson_lowlevel!(SolutionLow; μ = μ)
    @time solve_poisson_midlevel!(SolutionMid; μ = μ)
    @time solve_poisson_highlevel!(SolutionHigh; μ = μ)

    @show norm(SolutionLow.entries - SolutionHigh.entries)
    @show norm(SolutionLow.entries - SolutionMid.entries)

    # plot solution (for e.g. Plotter = PyPlot)
    p = GridVisualizer(; Plotter = Plotter, layout = (1,2), clear = true, resolution = (1000,500))
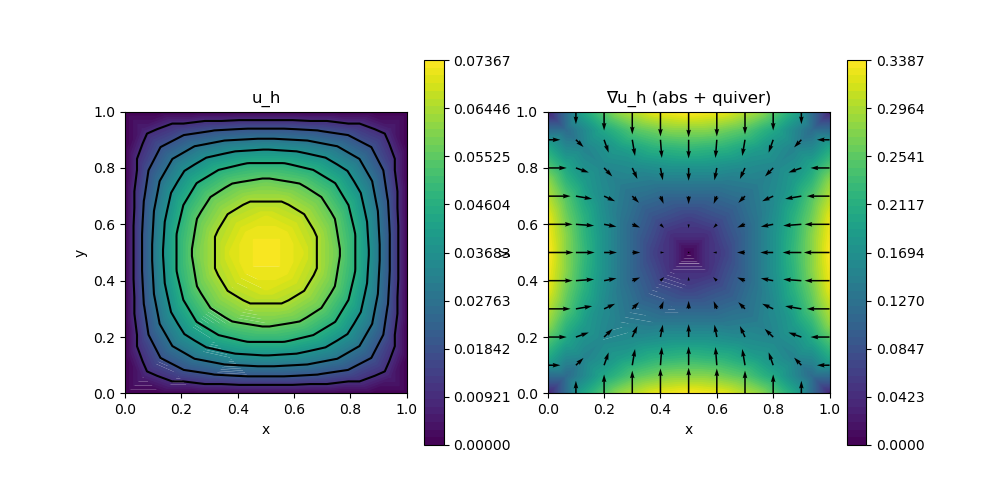
    scalarplot!(p[1,1], xgrid, view(nodevalues(SolutionLow[1]),1,:), levels = 7, title = "u_h")
    scalarplot!(p[1,2], xgrid, view(nodevalues(SolutionLow[1], Gradient; abs = true),1,:), vscale = 0.8, levels = 0, colorbarticks = 9, title = "∇u_h (abs + quiver)")
    vectorplot!(p[1,2], xgrid, evaluate(PointEvaluator(SolutionLow[1], Gradient)), spacing = 0.1, clear = false)
end


function assemble_Laplacian!(A::ExtendableSparseMatrix, FES; μ = 1)

    xgrid = FES.xgrid
    EG = xgrid[UniqueCellGeometries][1]
    FEType = eltype(FES)

    # quadrature formula
    qf = QuadratureRule{Float64, EG}(2*(get_polynomialorder(FEType, EG)-1))
    weights::Vector{Float64} = qf.w
    nweights::Int = length(weights)

    # dofmap
    CellDofs::Adjacency{Int32} = FES[GradientRobustMultiPhysics.CellDofs]
    ndofs4cell::Int = get_ndofs(ON_CELLS, FEType, EG)
    dof_j::Int, dof_k::Int = 0, 0

    # FE basis evaluator
    FEBasis_∇::FEEvaluator{Float64} = FEEvaluator(FES, Gradient, qf)
    ∇vals::Array{Float64,3} = FEBasis_∇.cvals

    # local matrix and vector structures
    Aloc = zeros(Float64, ndofs4cell, ndofs4cell)

    # ASSEMBLY LOOP
    ncells::Int = num_cells(xgrid)
    cellvolumes = xgrid[CellVolumes]

    @time for cell = 1 : ncells

        # update FE basis evaluators
        FEBasis_∇.citem[] = cell
        update_basis!(FEBasis_∇)

        for j = 1 : ndofs4cell
            for k = j : ndofs4cell
                temp = 0
                for qp = 1 : nweights
                    temp += weights[qp] * μ * dot(view(∇vals,:,j,qp), view(∇vals,:,k,qp))
                end
                Aloc[j,k] = temp
            end
        end

        Aloc .*= cellvolumes[cell]

        for j = 1 : ndofs4cell
            dof_j = CellDofs[j, cell]
            for k = j : ndofs4cell
                dof_k = CellDofs[k, cell]
                if abs(Aloc[j,k]) > 1e-14
                    # write into matrix, may cause allocations
                    rawupdateindex!(A, +, Aloc[j,k], dof_j, dof_k)
                    if k > j
                        rawupdateindex!(A, +, Aloc[j,k], dof_k, dof_j)
                    end
                end
            end
        end

        fill!(Aloc, 0)
    end
    flush!(A)
end

function assemble_rhs!(b::AbstractVector, FES::FESpace; f = nothing)

    if f === nothing
        fill!(b, 0)
        return
    end

    xgrid = FES.xgrid
    EG = xgrid[UniqueCellGeometries][1]
    FEType = eltype(FES)

    # quadrature formula
    qf = QuadratureRule{Float64, EG}(2*(get_polynomialorder(FEType, EG)-1))
    weights::Vector{Float64} = qf.w
    xref = qf.xref
    nweights::Int = length(weights)

    # dofmap
    CellDofs::Adjacency{Int32} = FES[GradientRobustMultiPhysics.CellDofs]
    ndofs4cell::Int = get_ndofs(ON_CELLS, FEType, EG)

    # FE basis evaluator
    FEBasis_id::FEEvaluator{Float64} = FEEvaluator(FES, Identity, qf)
    idvals::Array{Float64,3} = FEBasis_id.cvals
    L2G::L2GTransformer{Float64, Int32, EG} = L2GTransformer(EG, xgrid, ON_CELLS)

    # ASSEMBLY LOOP
    function barrier(L2G::L2GTransformer{Tv,Ti,Tg,Tc}) where {Tv,Ti,Tg,Tc}

        bloc = zeros(Float64, ndofs4cell)
        ncells::Int = num_cells(xgrid)
        dof_j::Int = 0
        x::Vector{Float64} = zeros(Float64, 2)
        cellvolumes = xgrid[CellVolumes]

        @time for cell = 1 : ncells
            for j = 1 : ndofs4cell
                # right-hand side
                temp = 0
                for qp = 1 : nweights
                    # get global x for quadrature point
                    update_trafo!(L2G, cell)
                    eval_trafo!(x, L2G, xref[qp])
                    # (f, v_j)
                    temp += weights[qp] * idvals[1, j, qp] * fdata(x)[1]
                end
                bloc[j] = temp
            end

            for j = 1 : ndofs4cell
                dof_j = CellDofs[j, cell]
                b[dof_j] += bloc[j] * cellvolumes[cell]
            end

            fill!(bloc, 0)
        end
    end
    barrier(L2G)
end

function solve_poisson_lowlevel!(Solution; μ = 1)
    @info "\nLOW - start\n=============="

    # init FEspace, matrix and right-hand side vector
    @info "LOW - assembly"
    @time begin
        FES = Solution[1].FES
        A = FEMatrix(FES, FES)
        b = FEVector(FES)
        assemble_Laplacian!(A.entries, FES; μ = μ)
        assemble_rhs!(b.entries, FES; f = f)
    end



    # fix boundary dofs
    @info "LOW - boundary data"
    @time begin
        BFaceDofs::Adjacency{Int32} = FES[GradientRobustMultiPhysics.BFaceDofs]
        nbfaces::Int = num_sources(BFaceDofs)
        AM::ExtendableSparseMatrix{Float64,Int64} = A.entries
        for bface = 1 : nbfaces
            for j = 1 : num_targets(BFaceDofs,bface)
                dof_j = BFaceDofs[j, bface]
                AM[dof_j,dof_j] = 1e60
                b.entries[dof_j] = 0
            end
        end
        ExtendableSparse.flush!(A.entries)
    end

    # solve
    @info "LOW - solve"
    @time Solution.entries .= A.entries \ b.entries

    @info "LOW - end"
end


function solve_poisson_midlevel!(Solution; μ = 1)
    @info "\nMID - start\n=============="
    @info "MID - assembly preparations"
    @time begin
        FES = Solution[1].FES
        A = FEMatrix(FES, FES)
        b = FEVector(FES)
        FEType = eltype(FES)
    end

    @info "MID - assembly A"
    @time assemble_operator!(A[1,1], LaplaceOperator(μ))
    @info "MID - assembly b"
    @time assemble_operator!(b[1], LinearForm(Identity, fdata; regions = [1]))

    # fix boundary dofs
    @info "MID - boundary data"
    @time begin
        BO = Array{BoundaryData, 1}(undef, 0)
        push!(BO, BoundaryData(HomogeneousDirichletBoundary; regions = [1,2,3,4]))
        fixed_dofs = boundarydata!(Solution[1], BO)
        @views b.entries[fixed_dofs] .= 1e60 * Solution.entries[fixed_dofs]
        apply_penalties!(A.entries, fixed_dofs, 1e60)
        ExtendableSparse.flush!(A.entries)
    end

    # solve
    @info "MID - solve"
    ExtendableSparse.flush!(A.entries)
    @time Solution.entries .= A.entries \ b.entries
    @info "MID - end"
end

function solve_poisson_highlevel!(Solution; μ = 1)
    @info "\nHIGH - start\n=============="
    # create PDE description
    @info "HIGH - problem description"
    @time begin
        Problem = PDEDescription("Poisson problem")
        add_unknown!(Problem; unknown_name = "u", equation_name = "Poisson equation")
        add_operator!(Problem, [1,1], LaplaceOperator(μ))
        add_rhsdata!(Problem, 1, LinearForm(Identity, fdata; regions = [1]))
        add_boundarydata!(Problem, 1, [1,2,3,4], HomogeneousDirichletBoundary)
    end

    # solve
    solve!(Solution, Problem; show_statistics = true)
    @info "HIGH - end"
end


end

This page was generated using Literate.jl.